Simple and Compound Interest

The  terms  interest,  interest period,  and   interest rate are useful in calculating equivalent sums of money for one interest period in the past and one period in the future. However, for more than one interest period, the terms simple interest and compound interest become important.

Simple interest  is calculated using the principal only, ignoring any interest accrued in preceding interest periods. The total simple interest over several periods is computed as

where I  is the amount of interest earned or paid and the interest rate i is expressed in decimal form.

EXAMPLE 1.14

GreenTree Financing lent an engineering company $100,000 to retrofi t an environmentally  unfriendly building. The loan is for 3 years at 10% per year simple interest. How much money  will the firm repay at the end of 3 years?

Solution

The interest accrued in the first year and in the second year does not earn interest. The interest due each year is $10,000 calculated only on the $100,000 loan principal.

In most financial and economic analyses, we use   compound interest   calculations.

For compound interest,  the interest accrued for each interest period is calculated on the principal plus the total amount of interest accumulated in all previous periods. Thus, compound interest means interest on top of interest.

Compound interest reflects the effect of the time value of money on the interest also. Now the interest for one period is calculated as

In mathematical terms, the interest It for time period t may be calculated using the relation.

EXAMPLE 1.15

Assume an engineering company borrows $100,000 at 10% per year compound interest and will pay the principal and all the interest after 3 years. Compute the annual interest and total  amount due after 3 years. Graph the interest and total owed for each year, and compare with the previous example that involved simple interest.

Solution

To include compounding of interest, the annual interest and total owed each year are calculated by Equation [1.8].

 The repayment plan requires no payment until year 3 when all interest and the principal, a total of $133,100, are due.  Figure 1–11  uses a cash flow diagram format to compare end-of-year  (a) simple and (b) compound interest and total amounts owed. The differences due to com- pounding are clear. An extra $133,100 – 130,000 = $3100 in interest is due for the  compounded  interest loan.

Note that while simple interest due each year is constant, the compounded interest due grows geometrically. Due to this geometric growth of compound interest, the difference between simple and compound interest accumulation increases rapidly as the time frame increases. For example, if the loan is for 10 years, not 3, the extra paid for compounding interest may be calculated to be $59,374.

Figure 1–11  Interest  I owed and total amount owed for (  a ) simple interest (Example 1.14) and (  b ) compound interest
(Example 1.15).  

A  more  effi  cient way to calculate the total amount due after a number of years in Example 1.15  is to utilize the fact that compound interest increases geometrically. This allows us to skip the  year-by-year computation of interest. In this case, the   total amount due at the end of each  year is

This allows future totals owed to be calculated directly without intermediate steps. The general form of the equation is

where i is expressed in decimal form. Equation [1.10] was applied above to obtain the  $133,100 due after 3 years. This fundamental relation will be used many times in the upcoming chapters.

We can combine the concepts of interest rate, compound interest, and equivalence to demon- strate that different loan repayment plans may be equivalent, but differ substantially in amounts  paid from one year to another and in the total repayment amount. This also shows that there are  many ways to take into account the time value of money.

EXAMPLE 1.16

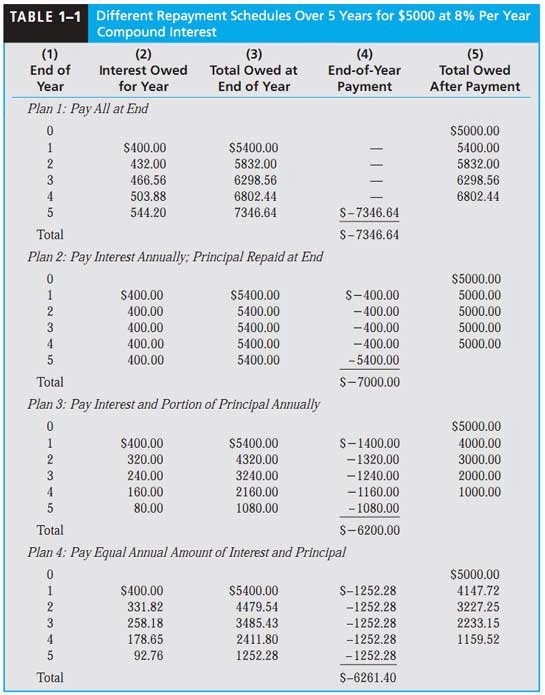
Table 1–1 details four different loan repayment plans described below. Each plan repays a  $5000 loan in 5 years at 8% per year compound interest. 

• Plan 1: Pay all at end.  No interest or principal is paid until the end of year 5. Interest accumulates each year on the total of principal and all accrued interest.
• Plan 2: Pay interest annually, principal repaid at end.  The accrued interest is paid each  year, and the entire principal is repaid at the end of year 5.
•  Plan 3: Pay interest and portion of principal annually.  The accrued interest and one-fi  fth  of the principal (or $1000) are repaid each year. The outstanding loan balance decreases  each year, so the interest (column 2) for each year decreases.
•  Plan 4: Pay equal amount of interest and principal.  Equal payments are made each year with a portion going toward principal repayment and the remainder covering the accrued interest. Since the loan balance decreases at a rate slower than that in plan 3 due to the equal  end-of-year payments, the interest decreases, but at a slower rate.

(a)  Make a statement about the   equivalence  of each plan at 8% compound interest.
(b)  Develop an 8% per year   simple  interest repayment plan for this loan using the same approach as plan 2. Comment on the total amounts repaid for the two plans.

Solution 

(a)  The amounts of the annual payments are different for each repayment schedule, and  the total amounts repaid for most plans are different, even though each repayment  plan  requires exactly 5 years. The difference in the total amounts repaid can be ex- plained by the time value of money and by the partial repayment of principal prior to  year 5.

A loan of $5000 at time 0 made at 8% per year compound interest is equivalent to each of the following:

Plan 1   $7346.64 at the end of year 5
Plan 2   $400 per year for 4 years and $5400 at the end of year 5
Plan 3    Decreasing payments of interest and partial principal in years 1 ($1400)  through 5 ($1080)
Plan 4   $1252.28 per year for 5 years  

An engineering economy study typically uses plan 4; interest is compounded, and a constant amount is paid each period. This amount covers accrued interest and a partial amount of principal repayment. 

(b) The repayment schedule for 8% per year simple interest is detailed in Table 1–2. Since  the annual accrued interest of $400 is paid each year and the principal of $5000 is repaid  in year 5, the schedule is exactly the same as that for 8% per year compound interest, and  the total amount repaid is the same at $7000. In this unusual case, simple and compound interest result in the same total repayment amount. Any deviation from this schedule will cause the two plans and amounts to differ.