Interest paid on borrowed funds (a loan) is determined using the original amount, also called the principal,
Interest = amount owed now - principal [1.1]
When interest paid over a specific time unit is expressed as a percentage of the principal, the result is called the interest rate.
The time unit of the rate is called the interest period. By far the most common interest period used to state an interest rate is 1 year. Shorter time periods can be used, such as 1% per month. Thus, the interest period of the interest rate should always be included. If only the rate is stated, for example, 8.5%, a 1-year interest period is assumed.
 |
| Figure 1–2 (a) Interest paid over time to lender. (b) Interest earned over time by investor. |
From the perspective of a saver, a lender, or an investor, interest earned ( Figure 1–2 b ) is the final amount minus the initial amount, or principal.
Interest earned total amount now principal [1.3]
Interest earned over a specific period of time is expressed as a percentage of the original amount and is called rate of return (ROR).
The time unit for rate of return is called the interest period, just as for the borrower’s perspec-
tive. Again, the most common period is 1 year.
The term return on investment (ROI) is used equivalently with ROR in different industries and settings, especially where large capital funds are committed to engineering-oriented programs.
The numerical values in Equations [1.2] and [1.4] are the same, but the term interest rate paid
is more appropriate for the borrower’s perspective, while the rate of return earned is better for
the investor’s perspective.
In Examples 1.3 to 1.5 the interest period was 1 year, and the interest amount was calculated at the end of one period. When more than one interest period is involved, e.g., the amount of interest after 3 years, it is necessary to state whether the interest is accrued on a simple or compound basis from one period to the next. This topic is covered later in this chapter.
Since inflation can significantly increase an interest rate, some comments about the funda- mentals of inflation are warranted at this early stage. By definition, inflation represents a decrease in the value of a given currency. That is, $10 now will not purchase the same amount of gasoline for your car (or most other things) as $10 did 10 years ago. The changing value of the currency affects market interest rates.
In simple terms, interest rates reflect two things: a so-called real rate of return plus the expected inflation rate. The real rate of return allows the investor to purchase more than he or she could have purchased before the investment, while inflation raises the real rate to the market rate that we use on a daily basis.
The safest investments (such as government bonds) typically have a 3% to 4% real rate of return built into their overall interest rates. Thus, a market interest rate of, say, 8% per year on a bond means that investors expect the inflation rate to be in the range of 4% to 5% per year. Clearly, inflation causes interest rates to rise.
From the borrower’s perspective, the rate of inflation is another interest rate tacked on to the real interest rate . And from the vantage point of the saver or investor in a fixed-interest account, inflation reduces the real rate of return on the investment. Inflation means that cost and revenue cash flow estimates increase over time. This increase is due to the changing value of money that is forced upon a country’s currency by inflation, thus making a unit of currency (such as the dollar) worth less relative to its value at a previous time. We see the effect of inflation in that money purchases less now than it did at a previous time. Inflation contributes to
• A reduction in purchasing power of the currency
• An increase in the CPI (consumer price index)
• An increase in the cost of equipment and its maintenance
• An increase in the cost of salaried professionals and hourly employees
• A reduction in the real rate of return on personal savings and certain corporate investments
In other words, inflation can materially contribute to changes in corporate and personal economic analysis.
Commonly, engineering economy studies assume that inflation affects all estimated values equally. Accordingly, an interest rate or rate of return, such as 8% per year, is applied throughout the analysis without accounting for an additional inflation rate. However, if inflation were explicitly taken into account, and it was reducing the value of money at, say, an average of 4% per year, then it would be necessary to perform the economic analysis using an inflated interest rate.
EXAMPLE 1.3
An employee at LaserKinetics.com borrows $10,000 on May 1 and must repay a total of $10,700 exactly 1 year later. Determine the interest amount and the interest rate paid.
Solution
The perspective here is that of the borrower since $10,700 repays a loan. Apply Equation [1.1] to determine the interest paid.
EXAMPLE 1.4
Stereophonics, Inc., plans to borrow $20,000 from a bank for 1 year at 9% interest for new recording equipment. ( a ) Compute the interest and the total amount due after 1 year. ( b ) Construct a column graph that shows the original loan amount and total amount due after 1 year used to compute the loan interest rate of 9% per year.
Solution
 |
| Figure 1–3 Values used to compute an interest rate of 9% per year. Example 1.4. |
Note that in part ( a ), the total amount due may also be computed as
Total due = principal(1 + interest rate) = $20,000(1.09) = $21,800
Later we will use this method to determine future amounts for times longer than one interest period.
EXAMPLE 1.5
(a) Calculate the amount deposited 1 year ago to have $1000 now at an interest rate of 5% per year. (b) Calculate the amount of interest earned during this time period.
Solution


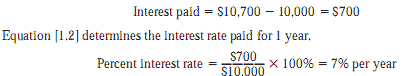


Awesome work! I am happy to get the thought of your article. It has data I have been hunting down quite a while. Church Financing
ReplyDeleteNeed a Debt Loan To Pay Off Bills?
ReplyDeleteTake control of your debt today
Available Now Business Expansion Loan Offer?
Do you need a loan to pay off Bills?
Do you need a loan?
Do you need Personal Loan?
Business Expansion Loan?
Business Start-up, Education,
Debt Consolidation Loan
Hard Money Loans
Loan for any thing ?
We offer loan at low interest rate of 3%
Loan with no credit check,
Email us: financialserviceoffer876@gmail.com
Call or add us on what's app +918929509036
All thanks to Mr Anderson for helping with my profits and making my fifth withdrawal possible. I'm here to share an amazing life changing opportunity with you. its called Bitcoin / Forex trading options. it is a highly lucrative business which can earn you as much as $2,570 in a week from an initial investment of just $200. I am living proof of this great business opportunity. If anyone is interested in trading on bitcoin or any cryptocurrency and want a successful trade without losing notify Mr Anderson now.Whatsapp: (+447883246472 )
ReplyDeleteEmail: tdameritrade077@gmail.com