Nominal and Effective Interest Rate Per Year.

Nominal interest rate per year, r, is the annual interest rate without considering the effect of any compounding.

In the example, the bank pays 21/2% interest every 6 months.The nominal interest rate per year, r, therefore, is 2 x 21/2%= 5%.

Effective interest rate per year, ia, is the annual interest rate taking into account the effect of any compoundingduring the year.

If a $1 deposit were made to an account that compounded interest m times per year and paid a nominal interest rate per year, r, the interest rate per compounding subperiowould be r/ m, and the total in the account at the end of one year would be

If we deduct the $1 principal sum, the expressionwould be

Therefore,

where i =effectiveinterest rate per compoundingsubperiod
m =number of compoundingsubperiodsper year

Either Equation4-32 or 4-33may be used to compute an effectiveinterest rate per year.

Oneshouldnote that i was describedin Chapter3 simplyas the interestrate per interest period.We were describing the effective interest rate without maldng any fuss about it.

A more precise definition,we now know, is that i is the effective interest rate per interest period. Although it seems more complicated,we are describing the same exact situation, but withmore care.

The nominalinterest rate r is often givenfor a one-yearperiod (but it couldbe givenfor either a shorter or a longer time period). In the specialcase of a nominal interest rate that is given per compoundingsubperiod, the effectiveinterest rate per compounding subperiod, i, equalsthe nominal interest rate per subperiod, r.

In thetypicaleffectiveinterestcomputation,there aremultiplecompoundingsubperiods (m > 1). The resulting effective interest rate is either the solution to the problem .or an intermediatesolution,whichallowsus to use standardcompoundinterest factors to proceed to solvethe problem.

For continuous compounding ,

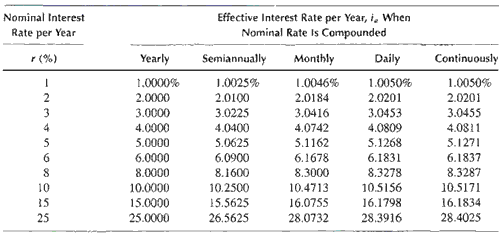
Table4-1 tabulates the effective interest rate for a range of compounding frequencies andnominal interest rates. It should be noted that when a nominal interest rate is compounded annually, the nominal interest rate equalsthe effective interest rate. Also, it will be noted that increasing the frequency of compounding (for example,from monthly to continuously) has only a small impact on the effective interest rate.But if the amount of money is large, evensmall differences in the effective interest rate canbe significant.

TABLE 4-1 Nominal and Effective Interest